![]()
Теоретическое обоснование гидравлического расчета
Гидропотери в трубопроводах систем водоснабжения вызваны гидравлическим сопротивлениям труб, смежных стыковых соединений, арматуры и прочих соединительных элементов. Калькулятор выполняет расчет только для простого (прямого) трубопровода, поэтому для сложных систем рекомендуется совершать вычисления для каждого отдельного участка.
Согласно методике СП 31.13330.2012 «Водоснабжение. Наружные сети и сооружения», гидравлический уклон (потери напора на единицу длины) определяется по формуле:
i = (λ / d) × (v2 / 2g)
- λ – коэффициент гидравлического сопротивления;
- d – внутренний диаметр труб, м;
- V – скорость воды, м/с;
- g – ускорение свободного падения, 9,81 м/с2.
Таким образом, из неизвестных остается только коэффициент гидравлического сопротивления, который рассчитывается по формуле:
λ = A1 × (A0 + C/V)m / dm
Коэффициенты А0, А1, С и значения показателя степени m соответствуют современным технологиям изготовления трубопроводов и принимаются согласно нижеуказанной таблицы. В случае, если эти параметры отличаются от перечисленных, производитель должен указывать их самостоятельно.
| Виды труб | m | A0 | A1 | С | |
| Новые стальные без внутреннего защитного покрытия или с битумным защитным покрытием | 0,226 | 1 | 0.0159 | 0.684 | |
| Новые чугунные без внутреннего защитного покрытия или с битумным защитным покрытием | 0,284 | 1 | 0.0144 | 2.360 | |
| Неновые стальные и неновые чугунные без внутреннего защитного покрытия или с битумным защитным покрытием | v < 1,2 м/с | 0,30 | 1 | 0.0179 | 0.867 |
| v ⩾ 1,2 м/с | 0,30 | 1 | 0.021 | 0.000 | |
| Асбестоцементные | 0,19 | 1 | 0.011 | 3.510 | |
| Железобетонные виброгидропрессованные | 0,19 | 1 | 0.01574 | 3.510 | |
| Железобетонные центрифугированные | 0,19 | 1 | 0.01385 | 3.510 | |
| Стальные и чугунные с внутренним пластмассовым или полимерцементным покрытием, нанесенным методом центрифугирования | 0,19 | 1 | 0.011 | 3.510 | |
| Стальные и чугунные с внутренним цементно-песчаным покрытием, нанесенным методом набрызга с последующим заглаживанием | 0,19 | 1 | 0.01574 | 3.510 | |
| Стальные и чугунные с внутренним цементно-песчаным покрытием, нанесенным методом центрифугирования | 0,19 | 1 | 0.01385 | 3.510 | |
| Пластмассовые | 0,226 | 0 | 0.01344 | 1.000 | |
| Стеклянные | 0,226 | 0 | 0.01461 | 1.000 | |
Расход воды в трубопроводе рассчитывается на основании известной усредненной скорости движения воды по трубе заданного сечения.
Q = π × (d2 / 4) × V / 1000
- d – внутренний диаметр трубопровода, мм;
- V – скорость потока жидкости, м/с.
Расчет гидравлического сопротивления и его роль
Любая трубопроводная коммуникация имеет не только прямолинейные участки, но и повороты, ответвления, для создания которых используются различные фитинги. А для регулирования потока рабочей среды устанавливается запорная арматура. Всё это создаёт сопротивление, поэтому очень важно перед тем, как приступать к монтажу трубопровода, необходимо выполнить ряд расчётов, в том числе определить гидравлическое сопротивление. Это позволит в будущем сократить теплопотери и, соответственно, избежать лишних энергозатрат.
Гидравлический расчёт выполняется с целью:
- Вычисления потерь давления на конкретных отрезках системы отопления;
- Определения оптимального диаметра трубопровода с учётом рекомендованной скорости перемещения рабочего потока;
- Расчёта тепловых потерь и величины наименьшего давления в трубопроводе;
- Правильного выполнения увязки параллельно расположенных гидравлических ветвей и закреплённой на ней запорной арматуры.
Во время движения по замкнутому контуру рабочему потоку приходится преодолевать определённое гидравлическое сопротивление. Причём с увеличением его значения, должна увеличиваться мощность насоса. Только правильные расчёты помогут выбрать оптимальный вариант насоса. Нет смысла покупать слишком мощное оборудования для трубопроводов с низким гидравлическим сопротивлением, ведь, чем больше мощность, тем выше энергозатраты.
А если мощность будет, наоборот, недостаточной, то насосное оборудование не сможет обеспечить достаточный напор теплоносителя, что приведёт к увеличению тепловых потерь.
Коэффициент гидравлического сопротивления трубы
Это безмерная величина, показывающая, каковы потери удельной энергии.
Ламинарное перемещение рабочего потока
При ламинарном (равномерном) перемещении рабочей среды по трубопроводу круглого сечения потери давления по длине вычисляется по формуле Дарси-Вейсбаха:
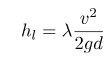
Где:
![]()
- потери давления по длине;
![]()
- коэффициент гидравлического сопротивления;
v – скорость движения рабочей среды;
g – ускорение силы тяжести;
d – диаметр трубопроводной магистрали.
Практически определено, что на коэффициент гидравлического сопротивления непосредственное влияние оказывает число Рейнольдса (Re) – безмерная величина, которая характеризует поток жидкости и выражается отношением динамического давления к касательному напряжению.
Если Re меньше, чем 2300, то для расчёта применяется формула:
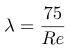
Для трубопроводов в форме круглого цилиндра:
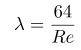
Для трубопроводных коммуникаций с другим (не круглым) сечением:
![]()
Где А=57 – для квадратных труб.
Турбулентное течение рабочего потока
При турбулентном (неравномерном, беспорядочном) перемещении рабочего потока коэффициент сопротивления вычисляют опытным путём, как функцию от Re. Если необходимо определить коэффициент гидравлического сопротивления для магистрали круглого сечения с гладкими поверхностями при
![]()
, то для расчёта применяется формула Блаузиуса:
![]()
В случае турбулентного перемещения рабочей среды на величину коэффициента трения влияет число Рейнольдса (характер течения) и насколько гладкая внутренняя поверхность трубопроводной коммуникации.
Коэффициент местного сопротивления
Это безмерная величина, которая устанавливается экспериментальным путём с помощью формулы:
![]()
Где:
![]()
– коэффициент местного сопротивления;
![]()
– потеря напора;
![]()
– отношение скорости потока к ускорению силы тяжести – скоростной поток.
При неизменной скорости перемещения рабочей среды по всему сечению применяется формула:
![]()
, где
![]()
– энергия торможения.
Коэффициент гидравлического сопротивления различных труб
Для фитингов из ППР:
| Муфта | 0,25 | ||
| Муфта переходная | Уменьшение на 1 размер | 0,40 | |
| Уменьшение на 2 размер | 0,50 | ||
| Уменьшение на 3 размер | 0,60 | ||
| Уменьшение на 4 размер | 0,70 | ||
| Угольник 90° | 1,20 | ||
| Угольник 45° | 0,50 | ||
| Тройник | Разделение потока | 1,20 | |
| Соединение потока | 0,80 | ||
| Крестовина | Соединение потока | 2,10 | |
| Разделение потока | 3,70 | ||
| Муфта комб. вн. рез. | 0,50 | ||
| Муфта комб. нар. рез | 0,70 | ||
| Угольник комб. вн. рез. | 1,40 | ||
| Угольник комб. нар. рез. | 1,60 | ||
| Тройник комб. вн. рез. | 1,40 - 1,80 | ||
| Вентиль | 20 мм | 9,50 | |
| 25 мм | 8,50 | ||
| 32 мм | 7,60 | ||
| 40 мм | 5,70 |
Для полиэтиленовых труб
| Сталь новая 133x5 | 60 | 1,4 | 3,6 |
| Сталь старая 133x5 | 60 | 1,4 | 6,84 |
| ПЭ 100 110x6,6 (5ЭР 17)/td> | 60 | 2,26 | 4,1 |
| ПЭ 80 110x8,1 (ЗйР 13,6) | 60 | 2,41 | 4,8 |
| Сталь новая 245x6 | 400 | 2,6 | 4,3 |
| Сталь старая 245x6 | 400 | 2,6 | 7,0 |
| ПЭ 100 225x13,4 (50 В 17) | 400 | 3,6 | 4,0 |
| ПЭ 80 225x16,6 (ЗЭК 13,6) | 400 | 3,85 | 4,8 |
| Сталь новая 630x10 | 3000 | 2,85 | 1,33 |
| Сталь старая 630x10 | 3000 | 2,85 | 1,98 |
| ПЭ 100 560x33,2 (ЗЭК 17) | 3000 | 4,35 | 1,96 |
| ПЭ 80 560x41,2 (ЗЭК 13,6) | 3000 | 4,65 | 2,3 |
| Сталь новая 820x12 | 4000 | 2,23 | 0,6 |
| Сталь старая 820x12 | 4000 | 2,23 | 0,87 |
| ПЭ100 800x47,4 (ЗЭК 17) | 4000 | 2,85 | 0,59 |
| ПЭ 80 800x58,8 (ЗЭР 13,6) | 4000 | 3,0 | 0,69 |
Для бесшовных стальных труб
| Ламинарный | или |
||
| Переходный | Проектирование трубопроводов не рекомендуется | ||
| Турбулентный | 1-я область |
(ф-ла Блазиуса) Бф-ла Конакова) |
|
| 2-я область |
(ф-ла Альтшуля) |
||
| 3-я область |
(ф-ла Альтшуля) (ф-ла Никурадзе) |
||
Для металлопластиковых труб
| Тройник разделения потока | 7,6 | |
| Тройник проходной | 4,2 | |
| Тройник противоположные потоки при разделении потока |
8,5 | |
| Тройник противоположные потоки при слиянии потока |
8,5 | |
| Угол 90° | 6,3 | |
| Дуга | 0,9 | |
| Редукционный переход | 6,3 | |
| Установочный уголок | 5,4 |
Трубы с низким коэффициентом гидравлического сопротивления
С точки зрения гидравлического сопротивления, наиболее оптимальными являются трубопроводные системы с гладкой внутренней стенкой:
aquatherm green pipe
Пластиковые трубы произведенные в Германии, широкого спектра применения.
Система отлично подходит для систем горячего и холодного водоснабжения и отопления, как в частных, так и промышленных масштабах. Так же используется для транспортировки химических сред.
Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.
Пластиковые трубы произведенные в Германии, широкого спектра применения.
Трубопроводная система из инновационного материала fusiolen, специально разработанная для систем холодоснабжения, обогрева поверхностей, транспортировки агрессивных сред и сжатого воздуха, а также для систем геотермальной энергетики.
Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.
Гидродинамический расчет трубопровода несжимаемой жидкости
При проведении гидродинамического расчета определяется значение числа Рейнольдса:
Re = W×D×ρ / μ;, где
μ – динамическая вязкость жидкости;
W – скорость потока;
D – диаметр трубопровода.
Определяется толщина ламинарного подслоя вдоль внутренней поверхности трубы:
δ = 68,4×Re-0.875×D / 2
В зависимости от величины шероховатости Δ внутренней поверхности трубы определяется коэффициент трения:
λ = 0,316×Re -0.25 при δ > Δ
λ = 0,11(Δ / D + 68 / Re) 0.25 при δ < Δ
По формуле Д’Арси определяется потеря давления на прямых участках:
ΔP = λ×(L / D)×(W2ρ / 2)
Потеря давления на местных сопротивлениях:
ΔP = ΣKi×(W2ρ / 2)
Суммируя полученные результаты, получают общую потерю давления на определенном участке трубопровода.
Расчет расхода газа и диаметра газопровода
Для расчета необходимого расхода газа необходимо указать тепловую мощность газовой котельной и ввести количество используемых на объекте газовых плит.
Для онлайн-расчета диаметра газопровода необходимо ввести расстояние от точки подключения газа до самой удаленной точки потребителя газа (газовой горелки, газовой плиты и т. п.).
| Введите тепловую мощность газовой котельной в кВт | кВт |
| Введите количество газовых плит (мощность 10 кВт), шт | шт. |
| Введите расстояние до самой удаленной точки потребителя газа, м | м |
| Расчетные показатели | Результаты |
| Общий расход газа 1 | м³/ч |
| Внутренний диаметр газопровода, мм 2 | мм |
Гидравлический расчет трубопроводов можно сделать самому
Трубопровод как способ транспортировки жидких и газообразных сред является самым экономичным способом во всех отраслях народного хозяйства. А значит он всегда будет пользоваться повышенным вниманием у специалистов.
Гидравлический расчет при проектировании трубопроводной системы позволяет определить внутренний диаметр труб и падение напора в случае максимальной пропускной способности трубы. При этом обязательным является наличие следующих параметров: материал, из которого изготовлены трубы, вид трубы, производительность, физико-химические свойства перекачиваемых сред.
Производя вычисления по формулам, часть заданных величин можно взять из справочной литературы. Ф.А.Шевелев, профессор, доктор технических наук разработал таблицы для точного расчета пропускной способности.
Теория
Труба представляет собой полый цилиндр из металла или другого материала. Применяют трубы для транспортировки жидких, газообразных и сыпучих сред.
Гидравлическое сопротивление — потери удельной энергии, которая переходит в теплоту, на участках гидравлических систем из-за вязкого трения.
Гидравлические потери бывают:
- трение по длине — появляются при равномерном течении, в чистом виде. В прямых трубах постоянного сечения, они пропорциональны длине трубы;
- местные гидравлические — возникает при изменении формы и размера канала, которые меняют поток. Пример: расширение трубы, сужение трубы, поворот, клапан.
Формула
Критерий Рейнольдса — характер потока вязкой жидкости:
- ρ — плотность жидкости,
- L — длина элемента потока,
- v — скорость потока,
- μ — динамический коэффициент вязкости.
- λ — коэффициент трения,
- k — коэффициент шероховатости трубы.
Потерю давления рассчитывают по формуле Хазена-Вильямса:
- ΔH – потери напора,
- С – коэффициент шероховатости Хазена-Вильямса,
- L – длина участка трубы,
- D – диаметр трубы,
- Q – расход.
Потери на трение, уравнение Дарси-Вейсбаха:
- ΔH — потери напора,
- L — длина участка трубы,
- d — диаметр трубы,
- λ — коэффициент трения,
- g — ускорение свободного падения,
- v — скорость потока.
Расчет падения давления:
∆p = λ · L/d · ρ/2 · v²
- Δp — перепад давления на участке трубы,
- λ — коэффициент трения,
- L — длина участка трубы,
- ρ — плотность перекачиваемой среды,
- d — диаметр трубы,
- v — скорость потока.
Постановка задачи
Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя. Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

Многолетний практический опыт эксплуатации систем трубопроводов показал, что трубы, имеющие круглое сечение, обладают определенными преимуществами перед трубопроводами, имеющими поперечное сечение любой другой геометрической формы:
- минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
- круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
- форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
- процесс изготовления труб круглой формы относительно простой и доступный.
Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.
Основными параметрами, характеризующими трубопровод являются:
- условный (номинальный) диаметр – DN;
- давление номинальное – PN;
- рабочее допустимое (избыточное) давление;
- материал трубопровода, линейное расширение, тепловое линейное расширение;
- физико-химические свойства рабочей среды;
- комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
- изоляционные материалы трубопровода.
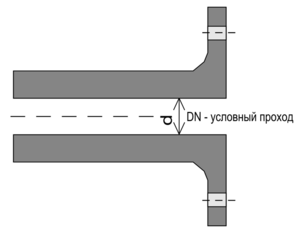
Условный диаметр (проход) трубопровода (DN) – это условная безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).
Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.
Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода. Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.
Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.
Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.
Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.
Основные положения гидравлического расчета
Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.
Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний, по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:

Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:
- ламинарный поток (Re<2300), при котором носитель-жидкость движется тонкими слоями, практически не смешивающимися друг с другом;
- переходный режим (2300
- турбулентный поток (Re>4000) – устойчивый режим, при котором в каждой отдельной точке потока происходит изменение его направления и скорости, что в итоге приводит к выравниванию скорости движения потока по объему трубы.
Критерий Рейнольдса зависит от напора, с которым насос перекачивает жидкость, вязкости носителя при рабочей температуре и геометрических размеров используемой трубы (d, длина). Данный критерий является параметром подобия для течения жидкости,поэтому, используя его, можно осуществлять моделирование реального технологического процесса в уменьшенном масштабе, что удобно при проведении испытаний и экспериментов.
Проводя расчеты и вычисления по уравнениям, часть заданных неизвестных величин можно взять из специальных справочных источников. Профессор, доктор технических наук Ф. А. Шевелев разработал ряд таблиц для проведения точного расчета пропускной способности трубы. Таблицы включают значения параметров, характеризующих как сам трубопровод (размеры, материалы), так и их взаимосвязь с физико-химическими свойствами носителя. Кроме того, в литературе приводится таблица приближенных значений скоростей движения потока жидкости, пара,газа в трубе различного сечения.
Подбор оптимального диаметра трубопровода
Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.
Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:
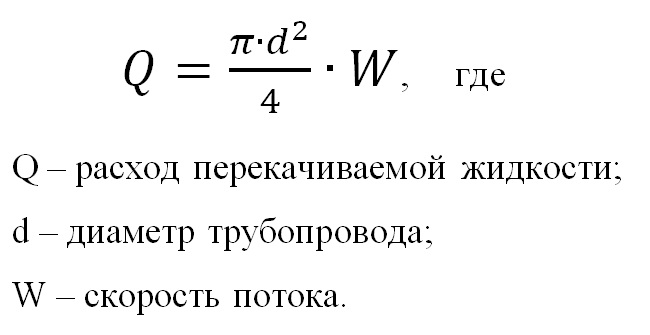
При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).
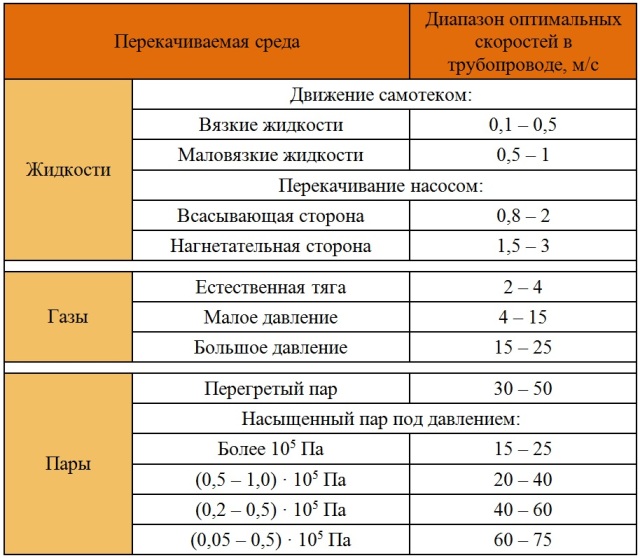
Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:

Расчет падения напора и гидравлического сопротивления
Полные потери напора жидкости включают в себя потери на преодоление потоком всех препятствий: наличие насосов, дюкеров, вентилей, колен, отводов, перепадов уровня при течении потока по трубопроводу, расположенному под углом и т.д. Учитываются потери на местные сопротивления, обусловленные свойствами используемых материалов.
Другим важным фактором, влияющим на потери напора, является трение движущегося потока о стенки трубопровода, которое характеризуется коэффициентом гидравлического сопротивления.
Значение коэффициента гидравлического сопротивления λзависит от режима движения потока и шероховатости материала стенок трубопровода. Под шероховатостью понимают дефекты и неровности внутренней поверхности трубы. Она может быть абсолютной и относительной. Шероховатость различна по форме и неравномерна по площади поверхности трубы. Поэтому в расчетах используется понятие усредненной шероховатости с поправочным коэффициентом (k1). Данная характеристика для конкретного трубопровода зависит от материала, продолжительности его эксплуатации, наличия различных коррозионных дефектов и других причин. Рассмотренные выше величины являются справочными.
Количественная связь между коэффициентом трения, числом Рейнольдса и шероховатостью определяется диаграммой Муди.
Для вычисления коэффициента трения турбулентного движения потока также используется уравнение Коулбрука-Уайта, с использованием которого возможно наглядное построение графических зависимостей, по которым определяется коэффициент трения:

В расчётах используются и другие уравнения приблизительного расчета потерь напора на трение. Одним из наиболее удобных и часто используемых в этом случае считается формула Дарси-Вейсбаха. Потери напора на трение рассматриваются как функция скорости жидкости от сопротивления трубы движению жидкости, выражаемой через значение шероховатости поверхности стенок трубы:

Потери давления по причине трения для воды рассчитывают по формуле Хазена — Вильямса:

Расчет потерь давления
Рабочее давление в трубопроводе – это на большее избыточное давление, при котором обеспечивается заданный режим технологического процесса. Минимальное и максимальное значения давления, а также физико-химические свойства рабочей среды, являются определяющими параметрами при расчёте расстояния между насосами, перекачивающими носитель, и производственной мощности.
Расчет потерь на падение давления в трубопроводе осуществляют по уравнению:

Примеры задач гидравлического расчета трубопровода с решениями
В аппарат с давлением 2,2 бар по горизонтальному трубопроводу с эффективным диаметром 24 мм из открытого хранилища насосом перекачивается вода. Расстояние до аппарата составляет 32 м. Расход жидкости задан – 80 м3/час. Суммарный напор составляет 20 м. Принятый коэффициент трения равен 0,028.
Рассчитайте потери напора жидкости на местные сопротивления в данном трубопроводе.
Исходные данные:
Расход Q = 80 м3/час = 80·1/3600 = 0,022 м3/с;
эффективный диаметр d = 24 мм;
длина трубы l = 32 м;
коэффициент трения λ = 0,028;
давление в аппарате Р = 2,2 бар = 2,2·105 Па;
общий напор Н = 20 м.
Решение задачи:
Скорость потока движения воды в трубопроводе рассчитывается по видоизмененному уравнению:
w=(4·Q) / (π·d2) = ((4·0,022) / (3,14·[0,024]2)) = 48,66 м/с
Потери напора жидкости в трубопроводе на трение определяются по уравнению:
HТ = (λ·l) / (d·[w2/(2·g)]) = (0,028·32) / (0,024·[48,66]2) / (2·9,81) = 0,31 м
Общие потери напора носителя рассчитываются по уравнению и составляют:
hп = H - [(p2-p1)/(ρ·g)] - Hг = 20 - [(2,2-1)·105)/(1000·9,81)] - 0 = 7,76 м
Потери напора на местные сопротивления определяется как разность:
7,76 - 0,31=7,45 м
Ответ: потери напора воды на местные сопротивления составляют 7,45 м.
Задача 2
По горизонтальному трубопроводу центробежным насосом транспортируется вода. Поток в трубе движется со скоростью 2,0 м/с. Общий напор составляет 8 м.
Найти минимальную длину прямого трубопровода, в центре которого установлен один вентиль. Забор воды осуществляется из открытого хранилища. Из трубы вода самотеком изливается в другую емкость. Рабочий диаметр трубопровода равен 0,1 м. Относительная шероховатость принимается равной 4·10-5.
Исходные данные:
Скорость потока жидкости W = 2,0 м/с;
диаметр трубы d = 100 мм;
общий напор Н = 8 м;
относительная шероховатость 4·10-5.
Решение задачи:
Согласно справочным данным в трубе диаметром 0,1 м коэффициенты местных сопротивлений для вентиля и выхода из трубы составляют соответственно 4,1 и 1.
Значение скоростного напора определяется по соотношению:
w2/(2·g) = 2,02/(2·9,81) = 0,204 м
Потери напора воды на местные сопротивления составят:
∑ζМС·[w2/(2·g)] = (4,1+1)·0,204 = 1,04 м
Суммарные потери напора носителя на сопротивление трению и местные сопротивления рассчитываются по уравнению общего напора для насоса (геометрическая высота Hг по условиям задачи равна 0):
hп = H - (p2-p1)/(ρ·g) - = 8 - ((1-1)·105)/(1000·9,81) - 0 = 8 м
Полученное значение потери напора носителя на трение составят:
8-1,04 = 6,96 м
Рассчитаем значение числа Рейнольдса для заданных условий течения потока (динамическая вязкость воды принимается равной 1·10-3 Па·с, плотность воды – 1000 кг/м3):
Re = (w·d·ρ)/μ = (2,0·0,1·1000)/(1·10-3) = 200000
Согласно рассчитанному значению Re, причем 2320
λ = 0,316/Re0,25 = 0,316/2000000,25 = 0,015
Преобразуем уравнение и найдем требуемую длину трубопровода из расчетной формулы потерь напора на трение:
l = (Hоб·d) / (λ·[w2/(2g)]) = (6,96·0,1) / (0,016·0,204) = 213,235 м
Ответ:требуемая длина трубопровода составит 213,235 м.
Задача 3
В производстве транспортируют воду при рабочей температуре 40°С с производственным расходом Q = 18 м3/час. Длина прямого трубопровода l = 26 м, материал - сталь. Абсолютная шероховатость (ε) принимается для стали по справочным источникам и составляет 50 мкм. Какой будет диаметр стальной трубы, если перепад давления на данном участке не превысит Δp = 0,01 мПа (ΔH = 1,2 м по воде)? Коэффициент трения принимается равным 0,026.
Исходные данные:
Расход Q = 18 м3/час = 0,005 м3/с;
длина трубопровода l=26 м;
для воды ρ = 1000 кг/м3, μ = 653,3·10-6 Па·с (при Т = 40°С);
шероховатость стальной трубыε = 50 мкм;
коэффициент трения λ = 0,026;
Δp=0,01 МПа;
ΔH=1,2 м.
Решение задачи:
Используя форму уравнения неразрывности W=Q/F и уравнение площади потока F=(π·d²)/4 преобразуем выражение Дарси – Вейсбаха:
∆H = λ·l/d·W²/(2·g) = λ·l/d·Q²/(2·g·F²) = λ·[(l·Q²)/(2·d·g·[(π·d²)/4]²)] = =(8·l·Q²)/(g·π²)·λ/d5 = (8·26·0.005²)/(9,81·3,14²)· λ/d5 = 5,376·10-5·λ/d5
Выразим диаметр:
d5 = (5,376·10-5·λ)/∆H = (5,376·10-5·0,026)/1,2 = 1,16·10-6
d = 5√1,16·10-6 = 0,065 м.
Ответ: оптимальный диаметр трубопровода составляет 0,065 м.
Исходные данные:
Q – расход потока жидкости в трубопроводе, в литрах в секунду;
ρ – плотность жидкости, в килограмм / метр 3 ;
ΔH – перепад высот начальной и конечной точки участка трубопровода, в метрах;
D – внутренний диаметр трубопровода, в миллиметрах;
L – длина трубопровода, в метрах;
Δ – абсолютная шероховатость внутренней стенки трубы, в миллиметрах.
Расход потока Q, л/c
Плотность жидкости ρ, кг/м 3
Динамическая вязкость жидкости μ, Па*с
Перепад высот трубопровода ΔH, м
Внутренний диаметр трубопровода D, мм
Длина трубопровода L, м
Коэффициент местных сопротивлений ΣKi
Абсолютная шероховатость Δ, мм
Статическое давление на входе Pс, Па
Динамическое давление Pд, Па
Полное давление на входе P, Па
Потери давления от трения ΔP, Па
Скорость потока W, м/с
Число Рейнольдса Re
Коэффициент трения λ
Толщина ламинарного подслоя δл, мм
Размер первой ячейки пристеночного слоя, мм
 Uteplim
Uteplim 3110
3110  ~9.5 мин
~9.5 мин









