Коэффициент расширения: что такое, для чего нужен и как рассчитать

Определение и формула коэффициента теплового расширения

Тепловым расширением называют изменение размеров тела при изменении его температуры. Тепловое расширение (сжатие) характеризуют при помощи соответствующего коэффициента. Различают линейное и объемное тепловое расширения. Эти процессы характеризуют коэффициентами теплового расширения:
— средний коэффициент линейного теплового расширения,
средний коэффициент объемного теплового расширения.

ОПРЕДЕЛЕНИЕКоэффициент теплового расширения — это физическая величина, которая характеризует изменение линейных размеров твердого тела с ростом или уменьшением его температуры.

Обозначим начальную длину тела
,
— его удлинение при увеличении температуры тела на
, тогда
будет равен:

Коэффициент линейного теплового расширения является характеристикой относительного удлинения (
), которое происходит при увеличении температуры тела на 1К.

При увеличении температуры увеличивается объем тела. Для твердых тел и жидкостей можно считать справедливой формулу:

где
— начальный объем тела,
— изменение температуры тела.

Коэффициент объемного расширения тела — это физическая величина, характеризующая относительное изменение объема тела (
), происходящее при нагревании тела на 1 K давление должно быть постоянным. Коэффициент
можно определить как:

Тепловое расширение твердого тела связывают с ангармоничностью тепловых колебаний частиц, составляющих кристаллическую решетку тела. В результате данных колебаний при увеличении температуры тела увеличивается равновесное расстояние между соседними частицами этого тела.

Изменение объема тела ведет к изменению его плотности:

где
— начальная плотность,
— плотность вещества при новой температуре. Так как величина
то выражение (4) иногда записывают как:

Коэффициенты теплового расширения зависят от вещества. В общем случае они будут зависеть от температуры. Коэффициенты теплового расширения считают независимыми от температуры в небольшом интервале температур.

Существует ряд веществ, имеющих отрицательный коэффициент теплового расширения. При повышении температуры такие материалы сжимаются. Обычно это происходит в узком интервале температур. Есть вещества, у которых коэффициент теплового расширения почти равен нулю в некотором определенном интервале.

Общие сведения

Коэффициент теплового расширения широко применяется в инженерных расчетах.

Для обозначения коэффициента теплового расширения обычно используют греческие буквы: β (для объемного расширения) и α (для линейного расширения). На сайте в расчетах применяется обозначение — bv и al соответственно.

Тепловое расширение твердых и жидких тел

Тепловое расширение (также используется термин «термическое расширение») — это изменение линейных размеров и формы тела при изменении его температуры. Количественно тепловое расширение жидкостей и газов при постоянном давлении характеризуется изобарным коэффициентом расширения (объёмным коэффициентом теплового расширения). Для характеристики теплового расширения твёрдых тел дополнительно вводят коэффициент линейного теплового расширения.

Для чего нужен коэффициент?

Коэффициент теплового расширения описывает, как изменяется размер объекта, когда происходит повышение его температуры. В зависимости от конкретного использования, коэффициент расширения может быть линейный или объемный. Если тело твердое, требуется узнать изменение его длины или конкретной области, поэтому применяется коэффициент линейного расширения. Для жидкостей и газов используется только температурное расширение, коэффициент линейного теплового расширения для них не подходит, потому что приобретают форму емкости, в которой находятся.

Коэффициент объемного теплового расширения показывает, какое относительное изменение объема тела при постоянном давлении и изменении его температуры на 1 градус. Выражается формулой:

Коэффициент линейного теплового расширения показывает относительное изменение длины тела, когда происходит его нагревание.

Выражается формулой:

Коэффициент линейного теплового расширения может иметь разные значения, если направления измерений будут разными.

Теоретически рассчитать коэффициент линейного объема можно, зная коэффициент объемного расширения (α V ≈ 3 α L).

При нагревании некоторых материалов происходит их сжатие, а не расширение. У них коэффициент расширения (линейный) будет иметь отрицательное значение, к примеру, вода (коэффициент расширения с отрицательным значением при температуре 0-3,984 °С).

Виды коэффициентов теплового расширения.

• • коэффициент объёмного теплового расширения;
  • коэффициент линейного теплового расширения.

Коэффициент объёмного теплового расширения

 К −1 (°C−1) — относительное изменение объёма тела при нагревании его на
градусов при постоянном давлении,и, для твёрдых тел

Коэффициент линейного теплового расширения

Коэффициент линейного теплового расширения показывает относительное изменение длины тела при нагревании на температуру ΔT:

 — относительное изменение линейного размера тела при нагревании его на dT градусов при постоянном давлении.

В общем случае, коэффициент линейного теплового расширения может быть различен при измерении вдоль разных направлений: αx, αy, αz. Для изотропных тел
и αV = 3αL;.

Например, вода, в зависимости от температуры, имеет коэффициент объёмного расширения

0,53·10−4 К-1 (при температуре 5-10 °C); 1,50·10−4 К-1 (при температуре 10-20 °C); 3,02·10−4 К-1 (при температуре 20-40 °C); 4,58·10−4 К-1 (при температуре 40-60 °C); 5,87·10−4 К-1 (при температуре 60-80 °C).

Для железа коэффициент линейного расширения равен 11,3×10−6 K−1

Связь коэффициентов теплового расширения

В первом приближении можно считать, что коэффициенты линейного и объемного расширения изотропного тела связаны соотношением:

Единицы измерения

Основной единицей измерения коэффициентов температурного расширения в системе СИ является:

Коэффициент объемного расширения и объем тела

Используя коэффициент объемного расширения можно записать формулу, которая позволяет рассчитать объем тела, если известны начальный объем и приращение температуры:

где
. Выражение (
) — называют биномом объемного расширения.

Тепловое расширение твердого тела связывают с ангармоничностью тепловых колебаний частиц, составляющих кристаллическую решетку тела. В результате данных колебаний при увеличении температуры тела увеличивается равновесное расстояние между соседними частицами этого тела.

Коэффициент объемного расширения и плотность вещества

Если при неизменной массе происходит изменение объема тела, то это приводит к изменению плотности его вещества:

где
— начальная плотность,
— плотность вещества при новой температуре. Так как величина
то выражение (4) иногда записывают как:

Формулы (3)-(5) можно использовать при нагревании тела и при его охлаждении.

Зависимость объёма тел от температуры

Частицы твёрдого тела занимают друг относительно друга определённые положения, но не остаются в покое, а совершают колебания. При нагревании тела увеличивается средняя скорость движения частиц. Средние расстояния между частицами при этом увеличиваются, поэтому увеличиваются линейные размеры тела, а следовательно, увеличивается и объём тела.

При охлаждении линейные размеры тела сокращаются, и объём его уменьшается.

При нагревании, как известно, тела расширяются, а при охлаждении сжимаются. Качественная сторона этих явлений была уже рассмотрена в начальном курсе физики.

Наша задача теперь — ознакомиться с количественными законами этих явлений.

Линейное расширение твёрдых тел

Твёрдое тело при данной температуре имеет определённую форму и определённые линейные размеры. Увеличение линейных размеров тела при нагревании называется тепловым линейным расширением.

Измерения показывают, что одно и то же тело расширяется при различных температурах по-разному: при высоких температурах обычно сильнее, чем при низких. Но это различие в расширении столь невелико, что при сравнительно небольших изменениях температуры им можно пренебречь и считать, что изменение размеров тела пропорционально изменению температуры.

В начальном курсе физики было установлено, что различные вещества по-разному расширяются при нагревании: одни сильнее, другие слабее; железо, например, расширяется сильнее стекла и слабее меди.

Чтобы количественно характеризовать это важное тепловое свойство тел, введена особая величина, называемая коэффициентом линейного расширения.

Пусть твёрдое тело при температуре 0°С имеет длину а при температуре t° его длина становится Значит, при изменении температуры на t° длина тела увеличивается на Предполагая, что увеличение длины при нагревании на каждый градус идёт равномерно, находим, что при нагревании на 1°С вся длина тела увеличилась на каждая единица длины на

Величина (греч. «бэта»), характеризующая тепловое расширение тела, называется коэффициентом линейного расширения.

Формула  показывает, что при t = 1°С и = 1 ед. длины величина равна т. е. коэффициент линейного расширения численно равен удлинению, которое получает при нагревании на 1°С стержень, имевший при 0°С длину, равную единице длины.

Из формулы следует, что наименованием коэффициента является

Формулу можно записать в следующем виде:

Отсюда легко определить длину тела при любой температуре, если известны его начальная длина и коэффициент линейного расширения.

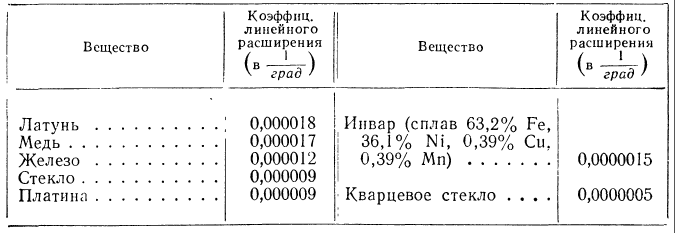
Ниже в таблице приведены коэффициенты линейного расширения некоторых веществ, определённые на опыте.

Объёмное расширение твёрдых тел

При тепловом расширении твёрдого тела с увеличением линейных размеров тела увеличивается и его объём. Аналогично коэффициенту линейного расширения для характеристики объёмного расширения можно ввести коэффициент объёмного расширения. Опыт показывает, что так же, как и в случае линейного расширения, можно без большой ошибки принять, что приращение объёма тела пропорционально повышению температуры.

Обозначив объём тела при 0°С через V0 , объём при температуре t0 через Vt а коэффициент объёмного расширения через найдём:

При V0 = 1 ед. объёма и t = 1°С величина а равна Vt— V0, т. е. коэффициент объёмного расширения численно равен приросту объёма тела при нагревании на 1°С, если при 0°С объём был равен единице объёма.

По формуле, зная объём тела при температуре 0°С, можно вычислить объём его при любой температуре t°:

Установим соотношение между коэффициентами объёмного и линейного расширения.

Допустим, что имеем кубик, ребро которого при 0° С равно 1 см. При нагревании на 1°С ребро станет равным см, а объём кубика увеличится на см3.

Можно написать следующее равенство:

Но

В этой формуле величины и настолько малы, что ими можно пренебречь и написать:

Коэффициент объёмного расширения твёрдого тела равен утроенному коэффициенту линейного расширения.

Учёт теплового расширения в технике

Из таблицы на странице 124 видно, что коэффициенты расширения твёрдых тел очень малы. Однако самые незначительные, изменения размеров тел при изменении температуры вызывают появление огромных сил.

Опыт показывает, что даже для небольшою удлинения твёрдого тела требуются огромные внешние силы. Так, например, чтобы увеличить длину стального стержня сечением в 1 см2 приблизительно на 0,0005 его первоначальной длины, необходимо приложить силу в 1000 кГ. Но такой же величины расширение этого стержня получается при нагревании его на 50°С. Ясно поэтому, что, расширяясь при нагревании (или сжимаясь при охлаждении) на 50°С, стержень будет оказывать давление около 1000 на те тела, которые будут препятствовать его расширению (сжатию).

Огромные силы, возникающие при расширении и сжатии твёрдых тел, учитываются в технике. Так, например, один из концов моста не закрепляют неподвижно, а устанавливают на катках; железнодорожные рельсы не укладывают вплотную, а оставляют между ними просвет; паропроводы подвешивают на крюках, а между отдельными трубами устанавливают компенсаторы, изгибающиеся при удлинении труб паропровода. По этой же причине котёл паровоза закрепляется только на одном конце, другой же его конец может свободно перемещаться.

Огромное значение имеет расширение от нагревания при точных измерениях. В самом деле, если масштабная линейка или калибр, которыми проверяются размеры изготовленной части машины, значительно изменяют свою величину, то необходимой точности при измерении не получится. Для избежания грубых ошибок при измерении или контроле изготовленные изделия заблаговременно приносят в помещение, где производятся измерения, чтобы они успели принять температуру калибров. Самые калибры и измерительные инструменты делают из материала с очень малым коэффициентом расширения. Таким материалом, например, является особая железо-никелевая сталь — инвар, с коэффициентом расширения 0,0000015.

Как показывает таблица на странице 124, платина и стекло имеют одинаковый коэффициент расширения; поэтому можно вплавлять платину в стекло, причём после охлаждения не происходит ни ослабления связи обоих веществ, ни растрескивания стекла. В электрических лампочках в стекло вплавляется железо-никелевая проволока, имеющая такой же коэффициент расширения, как и стекло. Заслуживает внимания очень малый коэффициент расширения у кварцевого стекла. Такое стекло выдерживает, не лопаясь и не растрескиваясь, неравномерное нагревание или охлаждение. Так, например, в раскалённую докрасна колбочку из кварцевого стекла можно вливать холодную воду, тогда как колба из обычного стекла при таком опыте лопается. Указанная особенность кварцевого стекла является следствием малости его коэффициента теплового расширения.

Применение и учет теплового расширения в быту и технике

БЕсли два, соединенных вместе материала находятся в среде с высокими перепадами температуры, то большая разность коэффициентов теплового расширения может повредить один или оба материала — то есть эти материалы будут подвергнуты термическому удару. Нередко в такой ситуации тепловое расширение вызывает ряд проблем, но в некоторых случаях, наоборот, удобно использовать материалы с разным коэффициентом теплового расширения. Хороший пример — термометры.

Термометры

В некоторых термометрах используют две соединенные между собой пластины с разным коэффициентом теплового расширения. Такую систему называют биметаллической пластиной. Длина пластин зависит от температуры, и они удлиняются или укорачиваются при повышении или понижении температуры. Разница в длине этих двух пластин соответствует разности температур, и термометр проградуирован соответственно. Биметаллическая пластина в термометре свернута в виде спирали, один конец которой закрепляется неподвижно, а другой, в виде стрелки, перемещается по шкале. При изменении температуры спираль раскручивается или скручивается.

Тепловое расширение используется также и в других термометрах. Жидкостные термометры состоят из емкости с жидкостью с высоким коэффициентом теплового расширения, например с ртутью или спиртом. К емкости прикреплена трубка, по которой жидкость поднимается при повышении температуры. Шкала проградуирована так, что высота, на которую поднимается жидкость, соответствует температуре.

По сравнению с ранними термометрами, конструкция современных термометров намного усовершенствована. Например, сегодня они показывают правильную температуру за несколько минут, в то время как ранним термометрам нужно было 20 минут и больше, чтобы прийти в равновесие с окружающей средой. На современных максимальных и минимальных термометрах, в отличие от нефиксирующих термометров, показания не меняются, пока их не сбросить вручную, например, встряхнув их, в случае со ртутными термометрами. Цифровые термометры также сохраняют минимальные и максимальные значения температуры в течение заданного периода времени.

В последнее время в интересах безопасности во многих странах постепенно заменяют домашние ртутные термометры спиртовыми. Это делается потому, что ртуть токсична, а уборка территории, загрязненной ртутью, если случайно разбить такой термометр, занимает много времени и дорого стоит, поэтому намного удобнее просто запретить ртутные термометры.

Терморегулятор

Две одинаковые полоски из разных металлов, например из железа и латуни, склёпанные вместе, образуют так называемую биметаллическую пластинку. При нагревании такие пластинки изгибаются вследствие того, что одна расширяется больше другой. Та из полосок, которая расширяется больше, оказывается всегда с выпуклой стороны. Это свойство биметаллических пластинок широко используется для измерения температуры и её регулирования.

1. Металлический термометр. Этот прибор представляет собой биметаллическую дугу (рис. 132, а), конец которой A прочно закреплён, а конец В свободен. Дуга соединена в В со стрелкой С. При изменении температуры дуга закручивается или раскручивается, двигая соответственно стрелку. Шкала проградуирована по обыкновенному термометру. Если к концу стрелки прикрепить перо, то колебания температуры можно записывать на специальной бумажной ленте. По такому принципу устроен термограф.

2. Термостат. Так называется прибор для установления постоянной температуры.

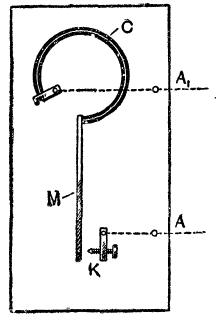
На рисунке  изображён принцип устройства одного из типов регуляторов температуры. Биметаллическая дуга С при изменении температуры закручивается или раскручивается. К её свободному концу прикреплена металлическая пластинка М, которая при раскручивании дуги прикасается к контакту К, а при закручивании отходит от него. Если, например, контакт К и пластинка М присоединены к концам электрической цепи АА1 содержащей нагревательный прибор, то при соприкосновении К и М электрическая цепь замкнётся; прибор начнёт нагревать помещение. Биметаллическая дуга С при нагревании начнёт закручиваться и при определённой температуре отсоединит пластинку М от контакта К цепь разорвётся, нагревание прекратится. При охлаждении дуга С, раскручиваясь, снова заставит включиться  нагревательный прибор: таким образом, температура помещения будет поддерживаться на заданном уровне.

Другие примеры

Ковар — пример материала с низким коэффициентом теплового расширения. Ковар — сплав никеля, кобальта и железа. Из него производят инструменты и детали, используемые в среде с высокими температурами. Благодаря низкой цене этого сплава и тому, что его тепловые свойства близки к свойствам боросиликатного стекла, его широко используют в лампах и электронных компонентах, например в электронно-лучевых и рентгеновских трубках, а также в магнетронах. Ковар обеспечивает механическое соединение между электрическими проводниками и стеклянной оболочкой электронных деталей.

Горячая запрессовка

Материалы с высоком коэффициентом теплового расширения удобно использовать в случае, если необходимо плотно надеть одну деталь на другую. Если детали, такие как трубы, нельзя соединить при обычной температуре, вставив одну в другую, то можно нагреть или охладить одну из труб, если она сделана из материала с высоким коэффициентом теплового расширения. При изменении температуры труба расширится или сузится и ее легко можно надеть сверху или вставить внутрь другой трубы. Этот процесс называется горячей запрессовкой

. Нередко в этой ситуации используют металлы, так как обычно их коэффициент теплового расширения высок. Горячую запрессовку можно проводить и с другими материалами. Материал изделия, которое нагревают или охлаждают, должен иметь высокий коэффициент теплового расширения в любом случае, но другая деталь может быть из дерева и другого теплостойкого материала.

[spoiler title="Источники"]

• http://ru.solverbook.com/spravochnik/koefficienty/koefficient-teplovogo-rasshireniya/
• https://gidrotgv.ru/spravka-po-koefficientu-teplovogo-rasshireniya-vidy-koefficientov-teplovogo-rasshireniya/
• https://natalibrilenova.ru/teplovoe-rasshirenie-tverdyih-i-zhidkih-tel/
• https://melt-spb.ru/vodoprovodnye/koefficient-linejnogo-rasshireniya.html
• https://dic.academic.ru/dic.nsf/ruwiki/78286
• http://ru.solverbook.com/spravochnik/koefficienty/koefficient-obemnogo-rasshireniya/
• https://WoodShpala.ru/proizvodstvo/koefficient-teplovogo-rasshireniya.html

[/spoiler]